Contents
Ejercicio 1
Imprimir una tabla formateada (entero y real) del logaritmo natural de los números 10, 20, 40, 60, y 80. Sugerencia: usar el comando fprintf y vectores
x=[10;20;40;60;80]; y=[x,log(x)]; fprintf('\n numero natural log\n') fprintf('%4i \t %8.3f\n',y')
numero natural log 10 2.303 20 2.996 40 3.689 60 4.094 80 4.382
ejercicio2
%Hallar el vector X para la siguiente ecuación matricial:
A=[4 -2 -10;2 10 -12;-4 -6 16];
b=[-10 32 -16]';
x=A\b
x1=inv(A)*b
x =
2.0000
4.0000
1.0000
x1 =
2
4
1
Ejercicio3
Para la matriz de coeficientes anterior hallar la factorización LU, es decir A = LU y aplicar a continuación X = U-1L-1B para resolver el sistema anterior.
[L U]=lu(A) x1=inv(U)*inv(L)*b
L =
1.0000 0 0
0.5000 1.0000 0
-1.0000 -0.7273 1.0000
U =
4.0000 -2.0000 -10.0000
0 11.0000 -7.0000
0 0 0.9091
x1 =
2
4
1
Ejercicio 4
%Hallar los autovalores y autovectores de la matriz A: A=[0 1 -1;-6 -11 6;-6 -11 5]; [X,D]=eig(A); fprintf('\n Autovectores (Columnas de la matriz)\n') X(:,1) fprintf('\n Autovalores (Diagonal)\n')
Autovectores (Columnas de la matriz)
ans =
0.7071
0.0000
0.7071
Autovalores (Diagonal)
Ejercicio 5
%calcular los voltajes de los nodods y la potencia de la fuente
Y=[1.5-2j -.35+1.2j;-.35+1.2j 0.9-1.6j];
I=[30+40j;20+15j]
V=Y\I
S=V.*conj(I)
I = 30.0000 +40.0000i 20.0000 +15.0000i V = 3.5902 +35.0928i 6.0155 +36.2212i S = 1.0e+03 * 1.5114 + 0.9092i 0.6636 + 0.6342i
Ejercicio 6
function TorresHanoi(n, i, a, f) if (n > 0) TorresHanoi(n-1, i, f, a); fprintf('mover disco %d de %c a %c\n', n, i, f); TorresHanoi(n-1, a, i, f);
end
TorresHanoi(5,'a','b','c')
mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 3 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c mover disco 4 de a a b mover disco 1 de c a b mover disco 2 de c a a mover disco 1 de b a a mover disco 3 de c a b mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 5 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c mover disco 3 de b a a mover disco 1 de c a b mover disco 2 de c a a mover disco 1 de b a a mover disco 4 de b a c mover disco 1 de a a c mover disco 2 de a a b mover disco 1 de c a b mover disco 3 de a a c mover disco 1 de b a a mover disco 2 de b a c mover disco 1 de a a c
Ejercicio 7
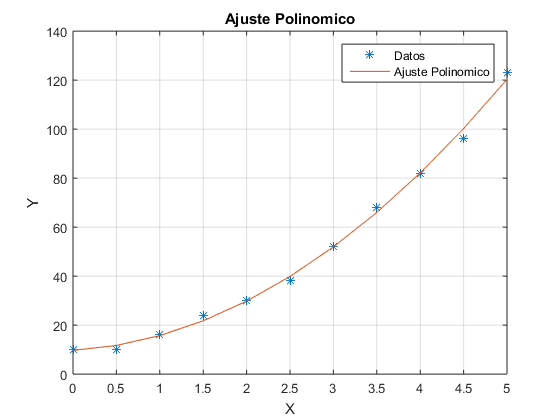
%ajuste de polinomio x=0:0.5:5; y=[10 10 16 24 30 38 52 68 82 96 123]; p=polyfit(x,y,2) yc=polyval(p,x) plot(x,y,'*',x,yc) xlabel('X'),ylabel('Y'),grid,title('Ajuste Polinomico') legend('Datos','Ajuste Polinomico',2)
p =
4.0233 2.0107 9.6783
yc =
Columns 1 through 7
9.6783 11.6895 15.7124 21.7469 29.7930 39.8508 51.9203
Columns 8 through 11
66.0014 82.0942 100.1986 120.3147
Ejercicio8
omegat=0:0.05:3*pi; v=120*sin(omegat); i=100*sin(omegat-(pi/4)); subplot(2,2,1) plot(omegat,v,omegat,i) title('Grafica Tensión e Intensidad'),xlabel('\omegat(radianes)') p=v.*i; subplot(2,2,2) plot(omegat,p) title('Potencia'),xlabel('\omegat (radianes)'),ylabel('watios') Fm=3.0; fa=Fm*sin(omegat); fb=Fm*sin(omegat-2*pi/3); fc=Fm*sin(omegat-4*pi/3); subplot(2,2,3) plot(omegat,fa,omegat,fb,omegat,fc) title('Fm trifasico'),xlabel('\omegat (radianes)') subplot(2,2,4) fr=3.0; plot(-fr*cos(omegat),fr*sin(omegat)) title('Radio fr')
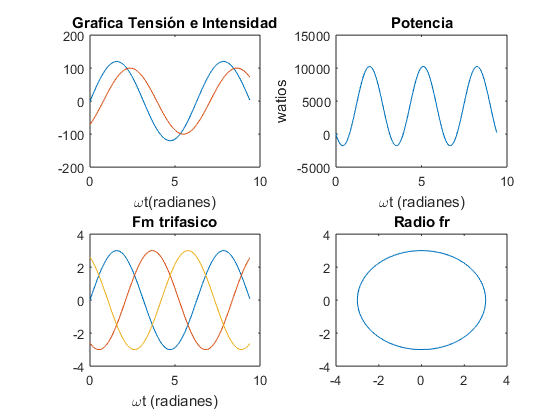
Ejercicio 9
t=linspace(0,16*pi,100) x=exp(-0.03.*t); y=exp(-0.03.*t); z=t; plot(t,x,t,y,t,z)
t =
Columns 1 through 7
0 0.5077 1.0155 1.5232 2.0309 2.5387 3.0464
Columns 8 through 14
3.5541 4.0619 4.5696 5.0773 5.5851 6.0928 6.6005
Columns 15 through 21
7.1083 7.6160 8.1237 8.6314 9.1392 9.6469 10.1546
Columns 22 through 28
10.6624 11.1701 11.6778 12.1856 12.6933 13.2010 13.7088
Columns 29 through 35
14.2165 14.7242 15.2320 15.7397 16.2474 16.7552 17.2629
Columns 36 through 42
17.7706 18.2784 18.7861 19.2938 19.8016 20.3093 20.8170
Columns 43 through 49
21.3248 21.8325 22.3402 22.8479 23.3557 23.8634 24.3711
Columns 50 through 56
24.8789 25.3866 25.8943 26.4021 26.9098 27.4175 27.9253
Columns 57 through 63
28.4330 28.9407 29.4485 29.9562 30.4639 30.9717 31.4794
Columns 64 through 70
31.9871 32.4949 33.0026 33.5103 34.0181 34.5258 35.0335
Columns 71 through 77
35.5413 36.0490 36.5567 37.0644 37.5722 38.0799 38.5876
Columns 78 through 84
39.0954 39.6031 40.1108 40.6186 41.1263 41.6340 42.1418
Columns 85 through 91
42.6495 43.1572 43.6650 44.1727 44.6804 45.1882 45.6959
Columns 92 through 98
46.2036 46.7114 47.2191 47.7268 48.2346 48.7423 49.2500
Columns 99 through 100
49.7578 50.2655
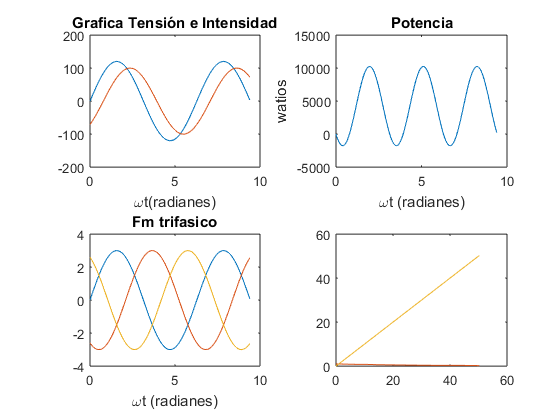
Ejercicio 10
x=-4:0.3:4; y=-4:0.3:4; z=sin(x).*cos(y).*exp(-(x.^2+y.^2).^0.5); plot(z)
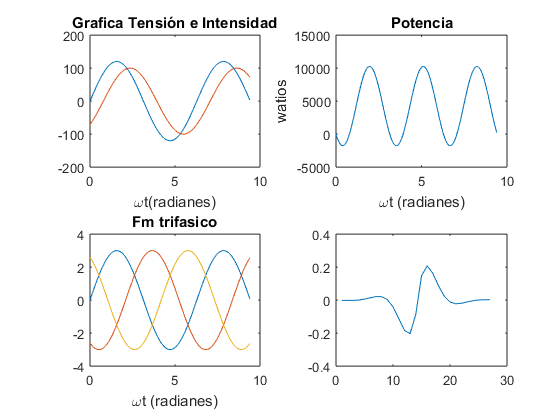
Ejercicio 11
%hallar las raices del polinomio
p=[1 0 -35 50 24];
r=roots(p)
r =
-6.4910
4.8706
2.0000
-0.3796
Ejercicio 12
%function y = HalfSine(t, y, z) %h = sin(pi*t/5).*(t<=5); %y = [y(2); -2*z*y(2)-y(1)+h]; [t, yy] = ode45(@HalfSine, [0 35], [1 0], [ ], 0.15); plot(t, yy(:,1))
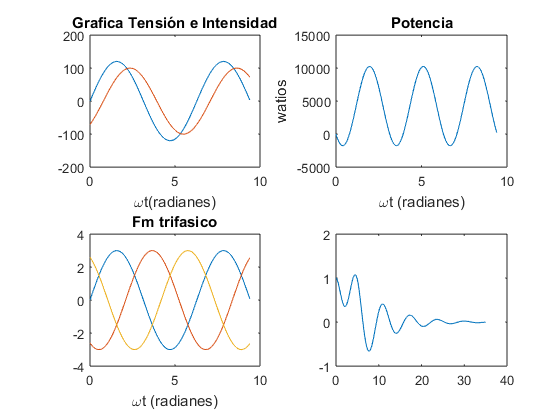
Ejercicio 13
k = 5; m = 10; fo = 10;Bo = 2.5; N = 2^m; T = 2^k/fo; ts = (0:N-1)*T/N; df = (0:N/2-1)/T; g1 = Bo*sin(2*pi*fo*ts)+Bo/2*sin(2*pi*fo*2*ts); An1 = abs(fft(g1, N))/N; plot(df, 2*An1(1:N/2)) g2 = exp(-2*ts).*sin(2*pi*fo*ts); An2 = abs(fft(g2, N))/N; plot(df, 2*An2(1:N/2)) g3 = sin(2*pi*fo*ts+5*sin(2*pi*(fo/10)*ts)); An3 = abs(fft(g3, N))/N; plot(df, 2*An3(1:N/2)) g4 = sin(2*pi*fo*ts-5*exp(-2*ts)); An4 = abs(fft(g4, N))/N; plot(df, 2*An4(1:N/2))
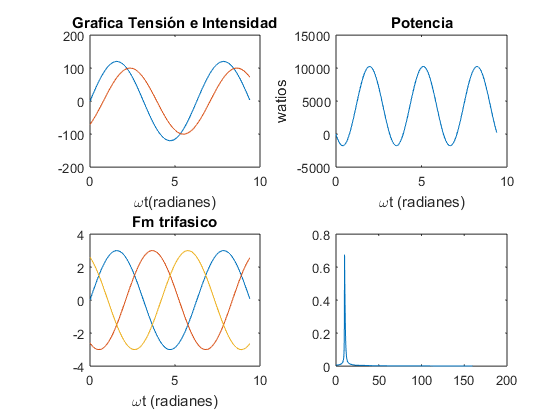
Ejercicio 14
subplot(1,1,1) A = imread('WindTunnel.jpg'); image(A) hold on figure r= A(200, :, 1); plot(r, 'r')

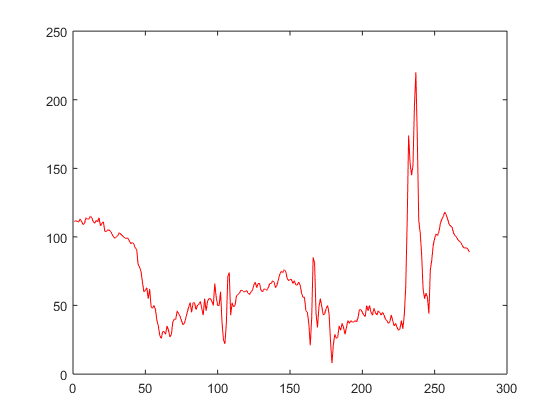
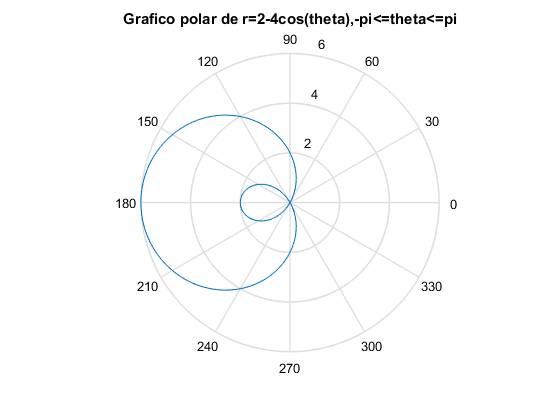
Ejercicio 15
theta = linspace(-pi, pi, 180);
r=2-4*cos(theta);
polar(theta,r)
title('Grafico polar de r=2-4cos(theta),-pi<=theta<=pi')